【平面几何】共用内切圆和外接圆三角形的透视

设△ABC的外接圆和内切圆分别是圆U和圆V。D是外接圆上的动点，D到内切圆的两条切线与外接圆交于E和F。请问，什么时候，△DEF和△ABC是透视对应？

工具/原料

电脑

网络画板

第一种情形

1、△DEF和△ABC关于直线UV对称。

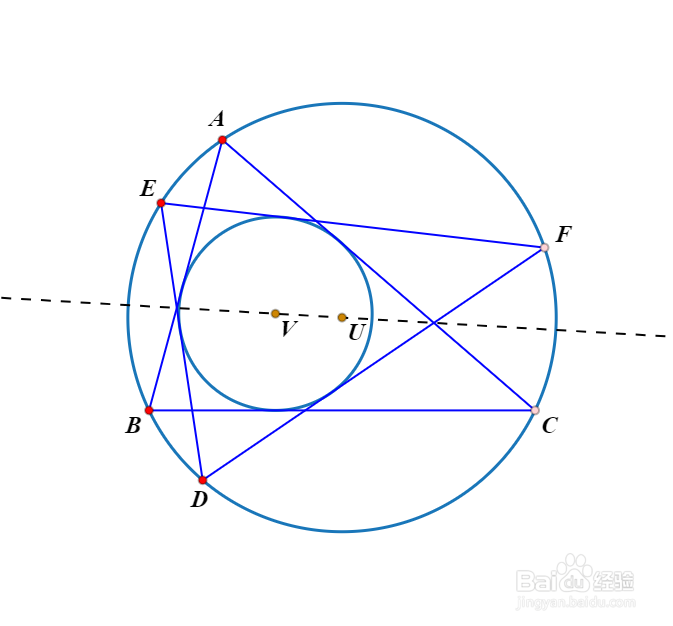
2、此时的透视中心是直线UV的垂线上的无限远点。

情形二

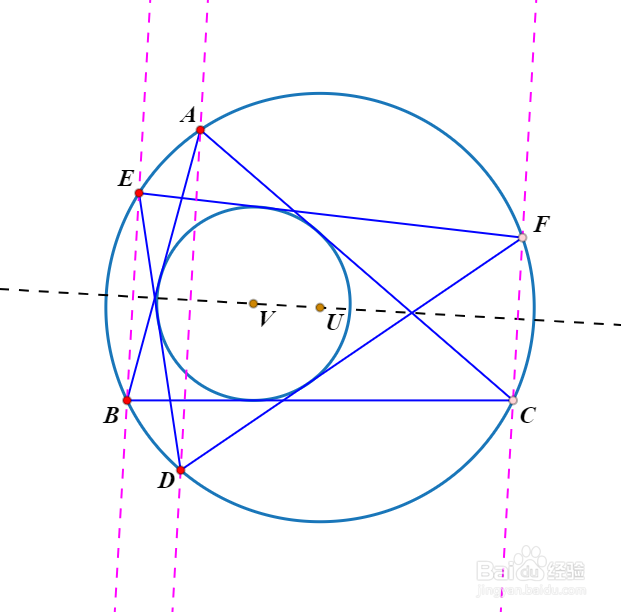
1、△ABC的Gergonne点X作为透视中心。

2、此时的点X实际上，是由△ABC的外接圆和内切圆产生的共轴圆系的一个极限点。至于极限点的作图方法，可以参考《怎么构造共轴圆系的极限点？》

情形三

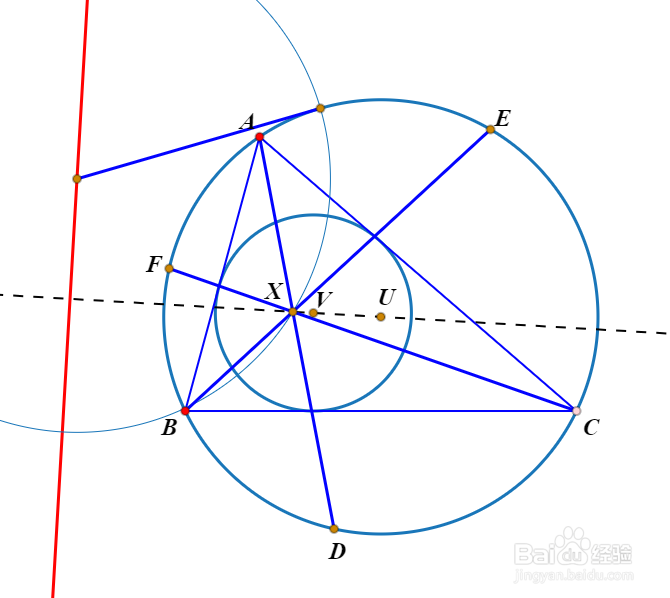
1、由△ABC的外接圆和内切圆产生的共轴圆系的第二个极限点，也可以作为透视中心。如下图的点Y。

2、此时的透视三角形DEF，如下图所示。